Analogue Filter Calculator

Calculate analogue filter parameters directly on this page.
Graph colours Red = Magnitude, Blue = Phase.
Complex frequency: s = σ + jω = σ + j·2π·f_o.

Passive Filters

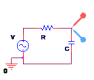
RC Circuits

[a] [b] [c]

Low-pass [a]

$H\(s\) = 1/{1 + s ⋅ R ⋅ C}$ $I_R = V/R \text" , " I_C = s ⋅ V ⋅ C$ $H\(s\) = {s ⋅ R ⋅ C}/{1 + s ⋅ R ⋅ C}$ $f_\o = 1/{2 ⋅ \π ⋅ R ⋅ C}$

R = Ω C = F fo = Hz τ = s

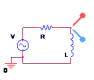
RL Circuits

[a] [b] [c]

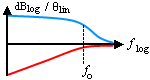High-pass [a]

$H\(s\) = {s ⋅ L}/{R + s ⋅ L}$ $I_R = V/R \text" , " I_L = V/{s ⋅ L}$ $H\(s\) = R/{R + s ⋅ L}$ $f_\o = R/{2 ⋅ \π ⋅ L}$

R = Ω L = H fo = Hz

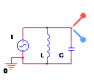
LC Circuits

[a] [b] [c]

Resonant (peak) [a]

$I_L = V/{s ⋅ L} \text" , " I_C = s ⋅ V ⋅ C$ $H\(s\) = 1/{s^2 ⋅ L ⋅ C + 1}$ $H\(s\) = {s^2 ⋅ L ⋅ C}/{s^2 ⋅ L ⋅ C + 1}$ $f_\o = 1/{2 ⋅ \π ⋅ √{L ⋅ C}}$

L = H C = F fo = Hz

Active Filters

OpAmp Low-pass/High-pass Circuits

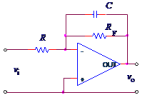
[a] [b]

Low-pass [a]

$H\(s\) = {-R_f}/R ⋅ 1/{1 + s ⋅ R_f ⋅ C}$ $H\(s\) = {-R_f}/R ⋅ {s ⋅ R_f ⋅ C}/{1 + s ⋅ R_f ⋅ C}$ $Gain = {-R_f}/R$ $f_\o = 1/{2 ⋅ \π ⋅ R_f ⋅ C}$

R = Ω C = F fo = Hz

OpAmp Circuit with Complex Poles

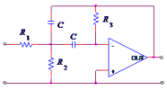
Band-pass with Q-factor and gain, G

$H(s) = {-(R_1 ⋅ C)^{-1} ⋅ s}/{s^2 + 2 ⋅ (R_3 ⋅ C)^{-1} ⋅ s + ({R_1 ⋅ R_2}/{R_1 + R_2} ⋅ R_3 ⋅ C^2)^{-1}}$ R1 = Q/G R2 = Q/(2 · Q2 - G) R3 = 2 · Q Resistor Scaling Factor = 1/(2 ·π· f0 · C)

fo = Hz Q = G = C = F R1 = Ω R2 = Ω R3 = Ω